Non-local Chemical Signals
Persistent Identifier
Use this permanent link to cite or share this Morpheus model:
Hybrid continuum-chemical and agent-based cell model
Introduction
The idea that the diffusion of extracellular signaling molecules sets up non-local cellular communications can also be used to simulate non-local forces using chemoattraction and repulsion.
Description
We compose a hybrid model with CPM cells that secrete two types of chemicals to which they respond chemotactically. We denote by $c_1$ the concentration field of the attractant, and by $c_2$ the repellent.
The is a simple generalization of the ‘Keller-Segel’ simulation to have two rather than a single chemical. While the Keller-Segel model (with its pure attraction of cells) could produce cell aggregation under the appropriate conditions, the interplay of both attraction and repulsion cues can account for a greater variety of behaviors.
Results
Cells each produce diffusible chemicals of two types, an attractant and a repellent. Depending on the relative rates of production, decay, and diffusion of attractant and repellent, the cells may either avoid each other (top), or cluster or aggregate (bottom).
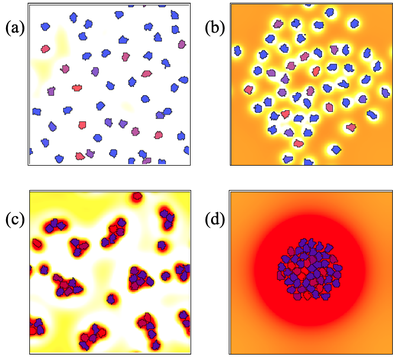
By adjusting the relative rates of diffusion (a.k.a. spatial ranges) and relative concentrations (a.k.a. magnitudes) of the corresponding ‘chemotactic forces’, we see distinct behaviors. Try the following experiments using model NonlocalChemSign.xml, which is set to behavior b) by default, to reproduce all behaviors shown in the figure above:
| Behavior | $\alpha_1$ | $\alpha_2$ | $\beta_1$ | $\beta_2$ | $D_1$ | $D_2$ |
|---|---|---|---|---|---|---|
| a) | $0.5$ | $0.5$ | $1$ | $0.1$ | $0.5$ | $1$ |
| b) | $0.05$ | $0.05$ | $2$ | $0.5$ | $1$ | $0.5$ |
| c) | $4$ | $0.5$ | $1$ | $0.1$ | $0.5$ | $1$ |
| d) | $0.5$ | $0.05$ | $0.01$ | $0.5$ | $1$ | $0.5$ |
NonlocalChemSign.xml ( | ) with the preset behavior b).
Model
NonlocalChemSign.xml
XML Preview
<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="4">
<Description>
<Title>Nonlocal Chemical Signaling</Title>
<Details>Full title: Non-local Chemical Signals
Authors: L. Edelstein-Keshet
Contributors: Y. Xiao
Date: 23.06.2022
Software: Morpheus (open-source). Download from https://morpheus.gitlab.io
Model ID: https://identifiers.org/morpheus/M2015
Reference: L. Edelstein-Keshet: Mathematical Models in Cell Biology
Comment: A group of cells that secrete both attractive and repulsive chemicals. Cells chemotax towards/away from the attractant/repellent. This hybrid cell-agent-based/chemical-continuum model mimics nonlocal interactions of cells (agents) with attraction-repulsion Morse potential. It can demonstrate cell clustering, cell spacing, and other dynamics. For distinct behaviours, try the following experiments: a) alpha_1 = 0.5, alpha_2 = 0.5, beta_1 = 1, beta_2 = 0.1, D1 = 0.5, D_2 = 1. b) alpha_1 = 0.05, alpha_2 = 0.05, beta_1 = 2, beta_2 = 0.5, D1 = 1, D_2 = 0.5. c) alpha_1 = 4, alpha_2 = 0.5, beta_1 = 1, beta_2 = 0.1, D1 = 0.5, D_2 = 1. d) alpha_1 = 0.5, alpha_2 = 0.05, beta_1 = 0.01, beta_2 = 0.5, D1 = 1, D_2 = 0.5.</Details>
</Description>
<Global>
<Field symbol="c1" name="attractant_1" value="0">
<Diffusion rate="1"/>
<Annotation>First define the chemical and set its boundary conditions. Also set the rate of diffusion of the chemical.
</Annotation>
</Field>
<Field symbol="c2" name="Repellent" value="0">
<Diffusion rate="0.5"/>
</Field>
<Field symbol="c" name="total stimulus" value="0">
<Diffusion rate="0"/>
</Field>
<System time-step="0.1" time-scaling="10" solver="Euler [fixed, O(1)]">
<Constant symbol="alpha1" value="0.05"/>
<Constant symbol="alpha2" value="0.05"/>
<Constant symbol="beta1" value="2"/>
<Constant symbol="beta2" value="0.5"/>
<DiffEqn symbol-ref="c1">
<Expression>is_source1*alpha1 - alpha2*c1</Expression>
<Annotation>The chemicals are produced at every point in space
where "is_source1" or "is_source2" is nonzero.
At every point in the region, the chemical will diffuse
and also decay at the rate called "decay".
</Annotation>
</DiffEqn>
<DiffEqn symbol-ref="c2">
<Expression>is_source2*beta1 - beta2*c2</Expression>
</DiffEqn>
</System>
<Equation symbol-ref="c" name="difference of two fields c1 and c2">
<Expression>c1-c2</Expression>
<Annotation>Lutz Brusch says: Algebraic equations must be given outside the <System...>
and will be evaluated as often as anything changes.
The "System" is reserved for differential equations
(and their constants and helper functions).
</Annotation>
</Equation>
</Global>
<Space>
<Lattice class="square">
<Size symbol="l" value="150, 150, 0"/>
<BoundaryConditions>
<Condition type="periodic" boundary="x"/>
<Condition type="periodic" boundary="y"/>
</BoundaryConditions>
<NodeLength value="0.1"/>
<Neighborhood>
<Distance>1.5</Distance>
</Neighborhood>
</Lattice>
<SpaceSymbol symbol="space"/>
</Space>
<Time>
<StartTime value="0"/>
<StopTime symbol="end" value="50"/>
<TimeSymbol symbol="time"/>
<RandomSeed value="124403"/>
</Time>
<CellTypes>
<CellType class="medium" name="medium">
<Property symbol="max_c1" value="0"/>
<Property symbol="max_c2" value="0"/>
<Property symbol="max_c" value="0"/>
<Property symbol="min_c" value="0"/>
<Property symbol="is_source1" value="0"/>
<Property symbol="is_source2" value="0"/>
<Annotation>The medium is not a source of any chemical.
Cells are sources of chemicals and are attracted to c=c1-c2 by chemotaxis
</Annotation>
</CellType>
<CellType class="biological" name="amoeba">
<VolumeConstraint target="40" strength="1"/>
<Chemotaxis strength="mu" field="c"/>
<Property symbol="is_source1" value="1"/>
<Property symbol="is_source2" value="1"/>
<Property symbol="max_c1" value="0"/>
<Property symbol="max_c2" value="0"/>
<Property symbol="max_c" value="0"/>
<Property symbol="min_c" value="0"/>
<Function symbol="mu">
<Expression>2</Expression>
</Function>
<Mapper>
<Input value="c"/>
<Output symbol-ref="max_c" mapping="maximum"/>
</Mapper>
<Mapper>
<Input value="c"/>
<Output symbol-ref="min_c" mapping="minimum"/>
</Mapper>
<Annotation>Cells are a source of both attractant and repellant. Mu sets the value of the chemotaxis rate.
</Annotation>
</CellType>
</CellTypes>
<CPM>
<Interaction>
<Contact type1="amoeba" type2="amoeba" value="6"/>
<Contact type1="amoeba" type2="medium" value="2"/>
</Interaction>
<MonteCarloSampler stepper="edgelist">
<MCSDuration symbol="MCStime" value="0.001875"/>
<Neighborhood>
<Order>2</Order>
</Neighborhood>
<MetropolisKinetics yield="0.1" temperature="1.0"/>
</MonteCarloSampler>
<ShapeSurface scaling="norm">
<Neighborhood>
<Distance>1.5</Distance>
</Neighborhood>
</ShapeSurface>
</CPM>
<CellPopulations>
<Population type="amoeba" size="1">
<InitCircle number-of-cells="50" mode="random">
<Dimensions radius="l.x/8" center="l.x/2, l.y/2, 0"/>
</InitCircle>
<Annotation>Initializes the cells to all be inside a little circle of radius 1/8 the domain size
</Annotation>
</Population>
</CellPopulations>
<Analysis>
<Gnuplotter time-step="1" decorate="false">
<Terminal size="400 400 0" name="png"/>
<Plot>
<Field symbol-ref="c" min="-0.5" max="0.5">
<ColorMap>
<Color value="-0.1" color="white"/>
<Color value="0" color="yellow"/>
<Color value="0.3" color="red"/>
</ColorMap>
</Field>
<Cells opacity="0.65" min="0.0" max="20" value="cell.id">
<ColorMap>
<Color value="1" color="red"/>
<Color value="50" color="blue"/>
</ColorMap>
</Cells>
</Plot>
</Gnuplotter>
<ModelGraph format="svg" reduced="false" include-tags="#untagged"/>
</Analysis>
</MorpheusModel>

Downloads
Files associated with this model: