Diffusion
Persistent Identifier
Use this permanent link to cite or share this Morpheus model:
Simulations of a diffusing field
Introduction
Here, we build up a simulation of diffusion over three successive files by:
- Starting with 1D and a short time scale in
Diffusion1a_main.xml( | ) , - simulating for longer times in
Diffusion1b.xml( | ) and - extending to 2D in
Diffusion2a.xml( | ) .
Description
Chemical diffusion and decay are easily simulated in Morpheus in 1D or 2D. We demonstrate the numerical simulation of the PDE and boundary conditions:
$$\begin{align} \frac{\partial c}{\partial t} = D \frac{\partial^2 c}{\partial x^2} - kc \quad c(0) = 0, c(L) = 5 \end{align}$$
Results
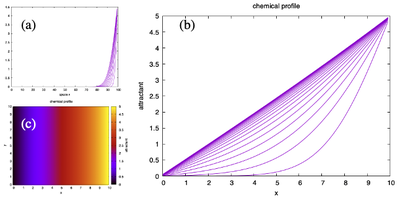
Diffusion1a_main.xml ( | )), (b) for longer times (Diffusion1b.xml ( | )), and (c) extension to 2D (Diffusion2a.xml ( | )).
Model
Diffusion1a_main.xml
XML Preview
<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="4">
<Description>
<Details>Full title: Diffusion
Authors: L. Edelstein-Keshet
Contributors: Y. Xiao
Date: 23.06.2022
Software: Morpheus (open-source). Download from https://morpheus.gitlab.io
Model ID: https://identifiers.org/morpheus/M2017
File type: Main model
Reference: L. Edelstein-Keshet: Mathematical Models in Cell Biology
Comment: A 1D domain with a chemical that diffuses at rate D and decays at rate k. Simple time plots in 1D of the chemical to show its diffusion into the domain.</Details>
<Title>Diffusion1a</Title>
</Description>
<Space>
<Lattice class="linear">
<Neighborhood>
<Order>1</Order>
</Neighborhood>
<Size symbol="size" value="100, 0, 0"/>
<BoundaryConditions>
<Condition type="constant" boundary="x"/>
<Condition type="constant" boundary="-x"/>
</BoundaryConditions>
</Lattice>
<SpaceSymbol symbol="space"/>
</Space>
<Time>
<StartTime value="0"/>
<StopTime value="50"/>
<TimeSymbol symbol="time"/>
</Time>
<Global>
<Field symbol="c" value="0">
<Diffusion rate="0.5"/>
<BoundaryValue boundary="x" value="5.0"/>
</Field>
<System time-step="0.5" solver="Runge-Kutta [fixed, O(4)]">
<DiffEqn symbol-ref="c" name="attractant">
<Expression>-k*c</Expression>
</DiffEqn>
<Constant symbol="k" name="decay rate" value="0.001"/>
</System>
</Global>
<Analysis>
<Logger time-step="5" name="chemical profile">
<Input>
<Symbol symbol-ref="c"/>
</Input>
<Output>
<TextOutput/>
</Output>
<Plots>
<Plot>
<Style style="lines"/>
<Terminal terminal="png"/>
<X-axis>
<Symbol symbol-ref="space.x"/>
</X-axis>
<Y-axis>
<Symbol symbol-ref="c"/>
</Y-axis>
</Plot>
</Plots>
</Logger>
<ModelGraph format="svg" reduced="false" include-tags="#untagged"/>
</Analysis>
</MorpheusModel>

Downloads
Files associated with this model: