Neural Stem Cell Redivisions in Adult Zebrafish Telencephalon

V. Lupperger, C. Marr, P. Chapouton (Authors)

DOI:10.1371/journal.pbio.3000708

Persistent Identifier

Use this permanent link to cite or share this Morpheus model:

Introduction

Whether individual stem cell divisions are coordinated or random is important for tissue morphogenesis, homeostasis and tumour growth. Lupperger et al. have analyzed the spatio-temporal division patterns of adult neural stem cells (NSC) in the zebrafish telencephalon. Imaging of over 80 000 NSCs in 36 brain hemispheres and comparison to model simulations with Morpheus revealed that redivisions (rapid cell cycle reentry by some newly born NSCs) can explain the observed aggregated division pattern.

Description

Units in the model are $[\text{space}] = \mathrm{\mu m}$, $[\text{time}] = 0.01\ \text{hours}$.
Parameter values were fitted by Lupperger et al. to in vivo labelling experiments. p_div = $9 \cdot 10^{−4}$ divisions per hour (amounts to $9 \cdot 10^{-6}$ divisions per Monte Carlo Step in the model) and p_rediv = $0.38$ (which can be adjusted in the model section Global). The differentiation process is set to $10\ %$.
Initial condition: $500$ cells, simulated until $2.356 \pm 460$ (mean ± SD) cells are reached, as in experiments.
The published model file was originally developed with Morpheus version 2.0.1 and is shared by the authors.
The new model file provided below has been updated (solver naming, added reference and links to description, moved parameters p_rediv, init_volume from CellType definition to Global to ease future modifications of their values) such that it works with Morpheus version 2.2.3 and later and reproduces the original results.

Results

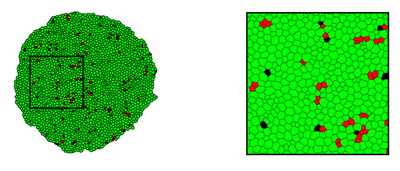
The model simulates the growth of the zebrafish telencephalon in a 2D cross section and visualizes NSCs in green, S-phase NSCs in red and progenitor cells in black as was presented in the published Figure S4G,H (shown below).

Running the model for 150 000 Monte Carlo steps (1 500 hours of brain development) yields 2 726 cells and reproduces the aggregated division pattern.

Model results reproduced with this Morpheus model. Figure was assembled from `plot-1*.png` and `plot-2*.pdf` output files.

The spatiotemporal dynamics from 20 000-150 000 Monte Carlo steps is shown in the following Video. The left panel shows each cell clone in a unique color and the right panel shows the cell states color-coded as in the above Figures.

Reference

This model is the original used in the publication, up to technical updates:

V. Lupperger, C. Marr, P. Chapouton: Reoccurring neural stem cell divisions in the adult zebrafish telencephalon are sufficient for the emergence of aggregated spatiotemporal patterns. PLoS Biology 18 (12): e3000708, 2020.

Model

Get this model via:

Morpheus-Link or

Download: model.xml

XML Preview

<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="4">
    <Description>
        <Title>Lupperger2020</Title>
        <Details>Full title:        Neural stem cell (NSC) redivisions in adult zebrafish telencephalon
Date: 	20.07.2021
Authors: 	V. Lupperger, C. Marr, P. Chapouton
Curators: 	V. Lupperger, L. Brusch
Software: 	Morpheus (open-source), download from https://morpheus.gitlab.io
ModelID: 	https://identifiers.org/morpheus/M2984
Reference:    This model is described in the peer-reviewed publication 
	V. Lupperger, C. Marr, P. Chapouton. Reoccurring neural stem cell divisions in the adult zebrafish telencephalon are sufficient for the emergence of aggregated spatiotemporal patterns. PLoS Biology 18 (12): e3000708, 2020. 
	https://doi.org/10.1371/journal.pbio.3000708
</Details>
    </Description>
    <Global>
        <Constant symbol="p_rediv" value="0.38"/>
        <Variable symbol="c" value="0.0"/>
        <Variable symbol="cellCycleTime" value="1e20"/>
        <Variable symbol="time_of_birth" value="0.0"/>
        <Variable symbol="p" value="2"/>
        <Variable symbol="progenitor" value="0"/>
        <Constant symbol="init_volume" value="50"/>
        <Variable symbol="volume" value="init_volume"/>
        <Variable symbol="minCellSize" value="25"/>
        <Variable symbol="maxCellSize" value="250"/>
        <Variable symbol="clone" value="0"/>
        <Variable symbol="cc" value="0"/>
    </Global>
    <Space>
        <Lattice class="hexagonal">
            <Size symbol="size" value="1500, 1500, 0"/>
            <BoundaryConditions>
                <Condition type="periodic" boundary="x"/>
                <Condition type="periodic" boundary="y"/>
            </BoundaryConditions>
            <Neighborhood>
                <Order>3</Order>
                <!--    <Disabled>
        <Distance>1</Distance>
    </Disabled>
-->
            </Neighborhood>
            <Annotation>spatial unit of one lattice step is \mathrm{\mu m}</Annotation>
        </Lattice>
        <SpaceSymbol symbol="space"/>
    </Space>
    <Time>
        <StartTime value="0"/>
        <StopTime symbol="stoptime" value="1.5e5">
            <Annotation>time unit is \mathrm{0.01 hours}</Annotation>
        </StopTime>
        <TimeSymbol symbol="time"/>
    </Time>
    <CellTypes>
        <CellType class="biological" name="cells">
            <Property symbol="maxCellSize" value="rand_norm(220,50)"/>
            <Property symbol="minCellSize" value="max(init_volume/2,30)"/>
            <Property symbol="volume" value="(maxCellSize-minCellSize)/(1+exp(-0.0005*((time-time_of_birth)-10000)))+minCellSize"/>
            <Property symbol="p" name="proliferation rate" value="9e-6&#xa;"/>
            <Property symbol="c" name="color" value="0"/>
            <VolumeConstraint strength="1" target="volume"/>
            <SurfaceConstraint strength="1" target="0.9" mode="aspherity"/>
            <System solver="Euler [fixed, O(1)]" time-step="1.0">
                <Rule symbol-ref="c">
                    <Expression>if( c > 0, c-1, 0)</Expression>
                </Rule>
                <Rule symbol-ref="volume">
                    <Expression>(maxCellSize-minCellSize)/(1+exp(-0.0005*((time-time_of_birth)-10000)))+minCellSize</Expression>
                </Rule>
                <Rule symbol-ref="progenitor">
                    <Expression>if(progenitor == 0,0,progenitor-1)</Expression>
                </Rule>
                <Rule symbol-ref="cc">
                    <Expression>if(progenitor >0, 2, c>0)</Expression>
                </Rule>
            </System>
            <CellDivision daughterID="daughter" division-plane="random" write-log="csv">
                <Condition>p>rand_uni(0,1) and((time-time_of_birth)==0 or ((time-time_of_birth)>cellCycleTime))</Condition>
                <Triggers>
                    <Rule symbol-ref="c" name="color after division">
                        <Expression>1900</Expression>
                    </Rule>
                    <Rule symbol-ref="p">
                        <Expression>if(mother2daughters&lt;p_rediv,p=1,p=9e-6)
</Expression>
                    </Rule>
                    <Rule symbol-ref="time_of_birth">
                        <Expression>time</Expression>
                    </Rule>
                    <Rule symbol-ref="cellCycleTime">
                        <Expression>(-(ln(rand_uni(0,1)))*85*100)+2215</Expression>
                    </Rule>
                    <!--    <Disabled>
        <Rule symbol-ref="progenitor">
            <Expression>if(daughter ==2 and sym_division >0.9,abs((mother2daughters&lt;0.45)-1)*rint(cellCycleTime),(mother2daughters&lt;0.45)*rint(cellCycleTime))
</Expression>
        </Rule>
    </Disabled>
-->
                    <Rule symbol-ref="minCellSize">
                        <Expression>volume/2</Expression>
                    </Rule>
                    <Rule symbol-ref="maxCellSize">
                        <Expression>rand_norm(220,50)</Expression>
                    </Rule>
                    <!--    <Disabled>
        <Rule symbol-ref="cellCycleTime">
            <Expression>if(daughter==2,rand_norm((-(ln(mother2daughters))*85*100)+2215,300),(-(ln(mother2daughters))*85*100)+2215)</Expression>
        </Rule>
    </Disabled>
-->
                    <Rule symbol-ref="progenitor">
                        <Expression>if(rand_uni(0,1)&lt;0.10,rint(cellCycleTime),0)</Expression>
                    </Rule>
                    <Rule symbol-ref="mother2daughters">
                        <Expression>rand_uni(0,1)</Expression>
                    </Rule>
                    <Rule symbol-ref="m2dProg">
                        <Expression>rand_uni(0,1)</Expression>
                    </Rule>
                </Triggers>
            </CellDivision>
            <CellDeath>
                <Condition>progenitor ==1 or (progenitor >1 and abs((time-time_of_birth)-cellCycleTime) &lt;3 )</Condition>
            </CellDeath>
            <Property symbol="clone" value="rand_uni(1,255)"/>
            <Property symbol="initialId" value="cell.id"/>
            <Property symbol="time_of_birth" value="0.0"/>
            <Property symbol="cellCycleTime" value="(-(ln(rand_uni(0,1)))*85*100)+2215"/>
            <Property symbol="progenitor" value="0.0"/>
            <Property symbol="mother2daughters" value="rand_uni(0,1)"/>
            <Property symbol="sym_division" value="rand_uni(0,1)"/>
            <Property symbol="cc" value="1"/>
            <Property symbol="m2dProg" value="rand_uni(0,1)"/>
        </CellType>
    </CellTypes>
    <CPM>
        <Interaction default="0">
            <Contact type1="cells" type2="cells" value="-4"/>
        </Interaction>
        <MonteCarloSampler stepper="edgelist">
            <MCSDuration value="1.0"/>
            <Neighborhood>
                <Order>2</Order>
            </Neighborhood>
            <MetropolisKinetics yield="0.1" temperature="3"/>
        </MonteCarloSampler>
        <ShapeSurface scaling="norm">
            <Neighborhood>
                <Order>3</Order>
            </Neighborhood>
        </ShapeSurface>
    </CPM>
    <CellPopulations>
        <Population type="cells" size="1">
            <InitCircle number-of-cells="500" mode="random">
                <Dimensions radius="100" center="750,750,0"/>
            </InitCircle>
        </Population>
    </CellPopulations>
    <Analysis>
        <Gnuplotter time-step="1000" decorate="false">
            <Terminal name="pdf"/>
            <Plot>
                <Cells min="0.0" max="1" value="c">
                    <ColorMap>
                        <Color color="red" value="1"/>
                        <Color color="green" value="0.0"/>
                    </ColorMap>
                </Cells>
                <!--    <Disabled>
        <CellLabels fontsize="4" value="0.0"/>
    </Disabled>
-->
            </Plot>
            <Plot>
                <Cells value="cc">
                    <ColorMap>
                        <Color color="red" value="1"/>
                        <Color color="green" value="0.0"/>
                        <Color color="black" value="2"/>
                    </ColorMap>
                </Cells>
                <!--    <Disabled>
        <CellLabels precision="0" fontsize="1" value="clone"/>
    </Disabled>
-->
            </Plot>
        </Gnuplotter>
        <Logger time-step="1000">
            <Input>
                <Symbol symbol-ref="celltype.cells.size"/>
                <Symbol symbol-ref="cell.center.x"/>
                <Symbol symbol-ref="cell.center.y"/>
                <Symbol symbol-ref="cellCycleTime"/>
                <Symbol symbol-ref="progenitor"/>
                <Symbol symbol-ref="cell.volume"/>
                <Symbol symbol-ref="clone"/>
                <!--    <Disabled>
        <Symbol symbol-ref="minCellSize"/>
    </Disabled>
-->
                <!--    <Disabled>
        <Symbol symbol-ref="maxCellSize"/>
    </Disabled>
-->
                <Symbol symbol-ref="p"/>
            </Input>
            <Output>
                <TextOutput/>
            </Output>
            <Plots>
                <Plot time-step="1000" log-commands="true">
                    <Style style="linespoints" grid="true" point-size="0.5"/>
                    <Terminal terminal="png"/>
                    <X-axis maximum="stoptime" minimum="0">
                        <Symbol symbol-ref="time"/>
                    </X-axis>
                    <Y-axis minimum="0">
                        <Symbol symbol-ref="celltype.cells.size"/>
                    </Y-axis>
                </Plot>
            </Plots>
        </Logger>
        <Gnuplotter time-step="1000" decorate="false">
            <Terminal name="png"/>
            <Plot>
                <Cells value="clone"/>
                <!--    <Disabled>
        <CellLabels precision="0" fontsize="1" fontcolor="white" value="clone"/>
    </Disabled>
-->
            </Plot>
            <Plot>
                <Cells value="cc">
                    <ColorMap>
                        <Color color="red" value="1"/>
                        <Color color="green" value="0.0"/>
                        <Color color="black" value="2"/>
                    </ColorMap>
                </Cells>
                <!--    <Disabled>
        <CellLabels precision="0" fontsize="1" value="clone"/>
    </Disabled>
-->
            </Plot>
        </Gnuplotter>
        <!--    <Disabled>
        <DependencyGraph format="svg"/>
    </Disabled>
-->
        <ModelGraph include-tags="#untagged" format="dot" reduced="false"/>
    </Analysis>
</MorpheusModel>

Downloads

Files associated with this model:

Brain Cell Cycle Cellular Potts Model CPM Neural Stem Cell NSC Parameter Optimization Progenitor Cell Published Models S-phase Spatio-Temporal Patterning Stem Cell Telencephalon Zebrafish

Last updated on Tue, 25 Apr 2023